Matplotlib

Google drive folder with Jupyter Notebooks used in class: Jupyter Notebooks from class

The matplotlib library is probably the single most used Python package for 2D-graphics. It provides both a quick way to visualize data from Python, and create publication-quality figures in many formats. We are going to explore Matplotlib in interactive mode covering most common cases. We will also look at the object oriented interface which provides more control and flexibility over the generated figures.

An extensive gallery of examples using Matplotlib can found at the Matplotlib examples page.

See also a summary of pyplot commands.

Some useful plotting options can also found in the SciPy lecture notes.

IPython

IPython is an enhanced interactive Python shell that has lots of interesting features including named inputs and outputs, access to shell commands, improved debugging and much more. When we start it with the command line argument --pylab, it allows interactive Matplotlib sessions that has Matlab/Mathematica-like functionality.

Matplotlib and pyplot

There are nice tools for making plots of 1d and 2d data (curves, contour plots, etc.) in the pyplot sub-module of Matplotlib.

To see some of what’s possible (and learn how to do it), visit the Matplotlib gallery. Clicking on a figure displays the Python code needed to create it.

The best way to get Matplotlib working interactively in a standard Python shell is to do

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> plt.interactive(True)
>>> x = np.linspace(-1, 1, 50)
>>> plt.plot(x, x**2, 'o-')

Notice also that, since pylab includes both matplotlib and numpy, you can get the exact same features using a more compact way as follows

>>> import pylab
>>> pylab.interactive(True)

Then you should be able to do

>>> x = pylab.linspace(-1, 1, 50)
>>> pylab.plot(x, x**2, 'o-')

and see a plot of a parabola appear.

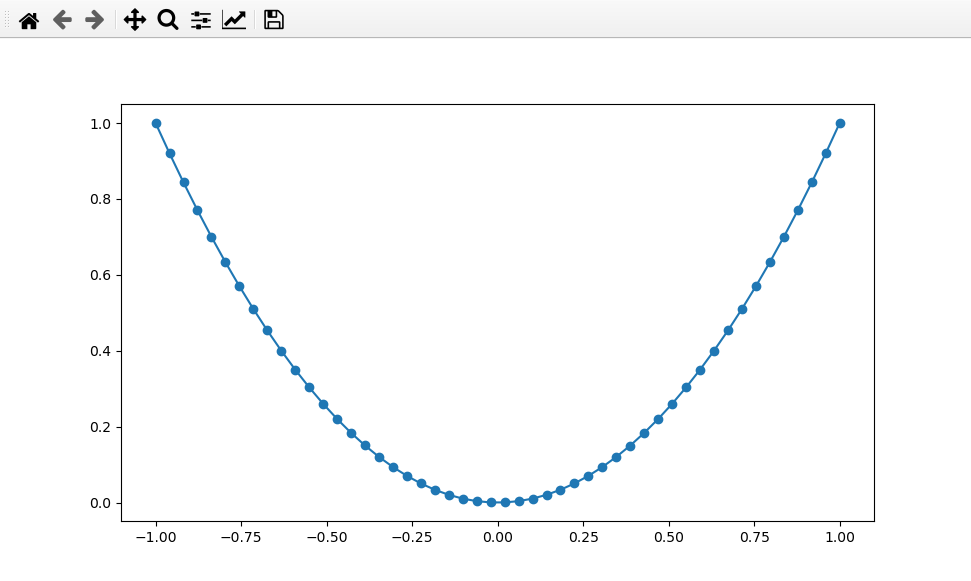
A simple plot of \(y = x^2\).

You should also be able to use the buttons on the window to interact with the plot, e.g. zoom in and out, change white space, change axis types, etc.

Alternatively, you could do

>>> from pylab import *
>>> interactive(True)

With this approach you don’t need to start every pylab function name with pylab, e.g.

>>> x = linspace(-1, 1, 50)
>>> plot(x, x**2, 'o-')

In these notes we’ll generally use module names just so it’s clear where things come from.

If you use the IPython shell instead, you can do

$ ipython --pylab

In [1]: x = linspace(-1, 1, 50)
In [2]: plot(x, x**2, 'o-')

The --pylab flag causes everything to be imported from pylab and set up for interactive plotting.

Matplotlib and Jupyter Notebooks

If you prefer to use Jupyter Notebooks you can get a more Matlab-like environment. In a cell of the Jupyter Notebook, type;

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt

And on the next cell,

x = np.linspace(-1, 1, 50)
plt.plot(x, x**2, 'o-')

When you execute the cell above, (by hitting ctrl+enter) you can see a figure as an output.

Labels, titles, grids, legends

Let’s continue with the plot of the parabola. Note that because we used plt.interactive(True) we can enter subsequent commands while the plot is already open.

First, add some axis labels and a plot title:

>>> plt.xlabel('x')
>>> plt.ylabel('y')
>>> plt.title(r'$y=x^2$')

Note

To use LaTex notation in Matplotlib plots you’ll need to use raw strings prefixed by an r as in the previous commands. Math mode can then be used safely by wrapping text with dollar signs. This is particularly needed when including Greek text or other items that would otherwise appear as escape codes. For example

>>> plt.xlabel(r'$\alpha$')
>>> # versus
>>> plt.xlabel('$\alpha$')

Those axis labels and the title are quite small. The xlabel, ylabel, and title functions can take in keyword arguments to control the text properties. Let’s change the axis labels to make everything larger:

>>> plt.xlabel(r'$x$',fontsize=16)
>>> plt.ylabel(r'$y$',fontsize=16)
>>> plt.title(r'$y=x^2$',fontsize=18)

Grid lines are often helpful to guide the viewer’s eye. These can be applied to major ticks, minor ticks, or both, and to the x-axis, y-axis, or both axes. For example

>>> plt.grid(which='both',axis='both')

After applying these changes you should have the following figure:

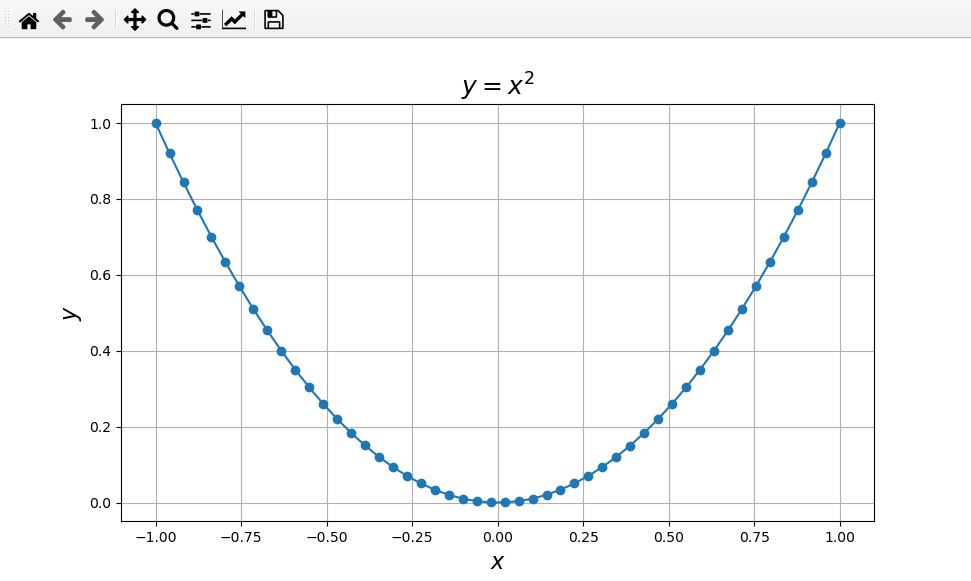
A simple plot of \(y = x^2\) with some nicer formatting.

Plotting multiple lines

We now consider an example of plotting more than one function in the same figure. In the script below, we’ve instantiated (and commented) all the figure settings that influence the appearance of the plot.

"""
/lectureNote/chapters/chapt05/codes/plot_sin_cos.py
The original code is from
http://www.scipy-lectures.org/intro/matplotlib/matplotlib.html
"""

# Slightly modified: Ian May Fall 2020, and again 2021

import numpy as np
import matplotlib.pyplot as plt

# Interactive defaults to False, we'll leave it that way
# Uncomment the following to change that
#plt.interactive(True)

# Instead of passing fontsize arguments all the time we can set them globally
plt.rc('axes',titlesize=14)
plt.rc('axes',labelsize=12)
plt.rc('xtick',labelsize=10)
plt.rc('ytick',labelsize=10)
plt.rc('legend',fontsize=8)

# Create a figure of size 8x6 inches, 200 dots per inch (the default is 100 dots/inch)
plt.figure(figsize=(8, 6), dpi=200)

# Set up a grid and some functions to plot
X = np.linspace(-np.pi, np.pi, 50)
C, S = np.cos(X), np.sin(X)

# Plot cosine with a blue continuous line of width 3.0 (pixels)
# Note that plot commands apply to the axis object
plt.plot(X, C, color="blue", linewidth=3.0, linestyle="-.")

# Plot sine with a green continuous line of width 2.5 and diamonds as markers
# compare format string '-gd' with individual keywords from previous call
plt.plot(X, S, '-gd', linewidth=2.5, markersize=5)

# Set axis labels
plt.xlabel(r'$x$')
plt.ylabel(r'$y$')

# Set x limits and tick positions/lebels
plt.xlim(-4.0, 4.0)
plt.xticks([-np.pi, -np.pi/2, 0, np.pi/2, np.pi], [r'$-\pi$', r'$-\pi/2$', r'$0$', r'$+\pi/2$', r'$+\pi$'])

# Set y limits and ticks
plt.ylim(-1.0, 1.0)
plt.yticks([-1, 0, +1], [r'$-1$', r'$0$', r'$+1$'])

# Set title
plt.title(r'$y=\sin(x)$ and $y=\cos(x)$ over $[-\pi, \pi]$')

# Set legend
# Note that line names are given as a tuple of strings
plt.legend((r'$\cos(x)$',r'$\sin(x)$'), loc='upper left')

# Show result on screen
# You need this when using plt.interactive(False)
plt.show()

Download this code

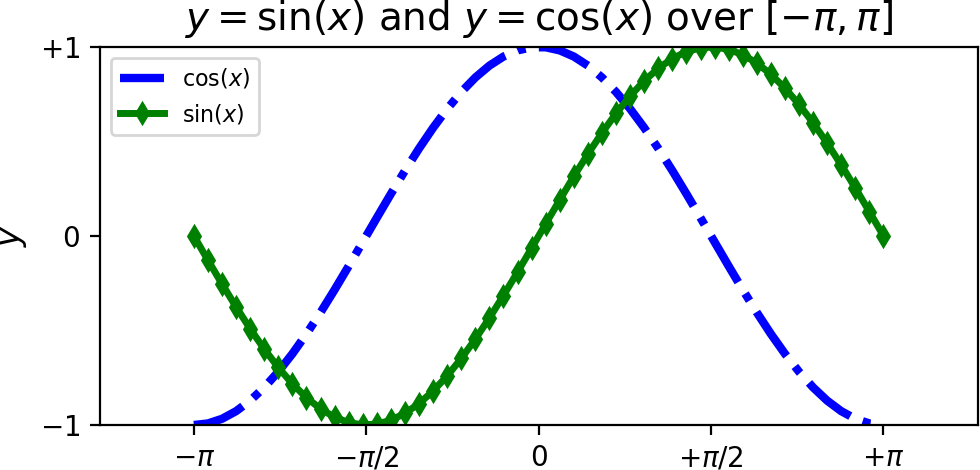
A figure of \(\sin(x)\) and \(\cos(x)\) functions over \([-\pi,\pi]\).

The next example demonstrates a simple way to read in some FLASH 2D data, extract a 1D slice, and plot a 1D density profile. The test problem is called the Shu-Osher shock tube problem, details of which are available at the FLASH users guide.

"""
/lectureNote/chapters/chapt04/codes/plot_flash_1d.py

An example Python 1d plotting code using a FLASH 2d data
-- The Shu-Osher hydrodynamics shock tube problem
   on a uniform grid of size 200 x 8


See more examples and options at:

  http://matplotlib.org/gallery.html
  http://matplotlib.org/users/image_tutorial.html

"""

import h5py
import numpy as np
import os
import sys
import matplotlib.pyplot as plt

def plot_flash_1d(file,yslice=0,var='dens',color='black') :
    var4plot = file[var]
    print(var4plot.shape)
    #plt.xlim(-4.5,4.5)
    dx = 9./200.
    x = np.linspace(-4.5 + 0.5*dx, 4.5, 200)
    plt.plot(x, var4plot[0,0,yslice,:],color=color,linewidth=2)  # plot a 1D section from a 2D data


# read in a data
dFile = h5py.File('ppm-hllc_hdf5_chk_0009', 'r')
print(dFile.keys())

# plot 1D graph
plot_flash_1d(dFile,yslice=4,var='dens',color='blue')
plot_flash_1d(dFile,yslice=4,var='pres',color='green')

# Enable gridlines
plt.grid(True)

# Set x label
plt.xlabel('$x$')

# Set y label
plt.ylabel(r'$\rho$, $p$')

# legend
plt.legend((r'density, $\rho$', r'pressure, $p$'), loc='center left')

# show to screen
plt.show()

# close the file
dFile.close()

Download this code

Download the hdf5 data file

Note

After downloading the data file, you may need to remove the file extension .txt if it has one.)

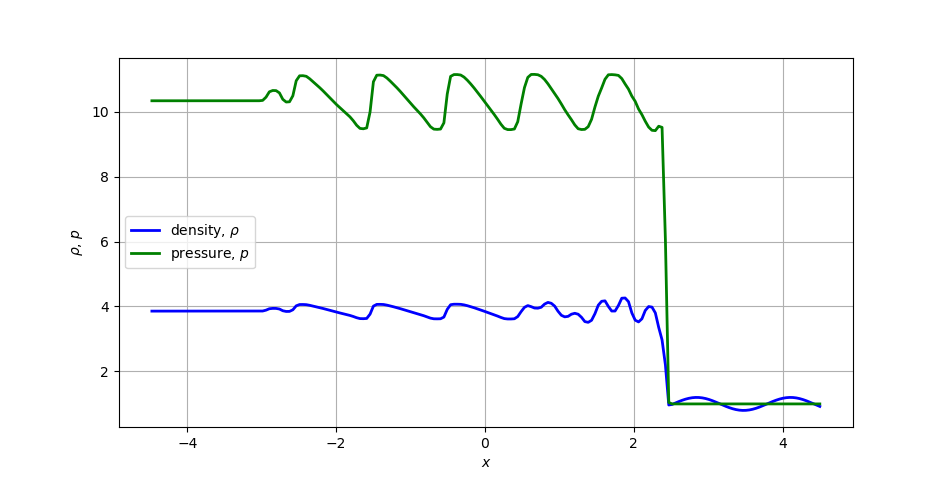
1D density and pressure profiles for the Shu-Osher shock tube problem.

Exercise: Return to finite difference approximations

We finished the NumPy section with three example codes, the first of which was An example: Numerical differentiation. Return to that example, and add plots of the exact and approximate derivatives, as well as plots for the error in the approximation. In particular, do the following:

• On one plot show the exact first derivative and both approximations

  • Use different line styles for each line and add a legend

  • Plot the error on the same plot using a second y-axis

• Repeat for the second derivative

Plotting the error on the same figure using a different scale requires us to dig a little deeper into how figures are created. In this case we’ll pull out the figure and axis objects explicitly and work with them. Consider the following code snippet:

# Generate plots
fig, ax = plt.subplots()
# Deriv and approximations
ax.plot(xf,ex_fFD,'-k',xf,fFD,'-b',xc,cFD,'-r')
ax.legend(('Exact','Fwd. Diff.','Ctr. Diff.'),loc='upper left')
ax.set_xlabel('x',fontsize=14)
ax.set_ylabel('Derivative',fontsize=14)
ax.set_title('Finite difference approximation',fontsize=16)
ax.grid('both')
# Create second axis for the error
# Note that we clone the x-axis instead of making a new y-axis
ax_err = ax.twinx()
ax_err.plot(xf,np.abs(fFD - ex_fFD),'--b',xc,np.abs(cFD - ex_cFD),'--r')
ax_err.set_ylabel('Absolute error')

fig.tight_layout()
plt.show()

Here we call plot directly on the axis object, instead of working through the static interface plt.*. Most of the functions are the same, but note the set_ prefix on the label and title functions. This approach requires a little more set up, but allows much greater flexibility in what you can plot.

Advanced plots – 2D plots, 3D plots, subplots and more

So far we have covered some basic features for producing plots from 1D data. Let’s briefly take a look at an example which produces 2D plots of a Rayleigh-Taylor instability. This is an unstable configuration where a heavy fluid lies above a light fluid in the presence gravity. See the wiki page for more information.

To do this we’ll use this plotting script which manages all of the HDF5 file format stuff and pulls out the individual fields.

# Author: Ian May
# File: gpplot.py
# Purpose: Make plots and movies from solution files generated
#          by my GP-WENO code

import numpy as np
import h5py
import glob
import matplotlib.pyplot as plt
import sys

# Return hdf5 dictionary corresponding to a single file
def dataFromFile(fStr):
    print('Opening ', fStr)
    f = h5py.File(fStr,'r')
    data = {}
    for k in f.keys():
        data[k] = f[k][()]
    data['ext'] = tuple(data['ext'])
    if 'time' in data:
        data['time'] = data['time'][0]
    data['filename'] = f.filename
    f.close()
    return data

# Return a list of hdf5 dictionaries for all file matching a glob
def dataFromGlob(gStr):
    dset = []
    for fStr in glob.iglob(gStr):
        dset.append(dataFromFile(fStr))
    return dset

# Plot a single field from one dataset
# Optionally supply fname to override showing the plot window
#   saving directly to a file
def plotField(d,fld,nCont=0,cmap='jet',fname='',vr=[]):
    plt.figure(figsize=(9.6,5.4),dpi=200)
    if len(vr)==2:
        plt.imshow(d[fld],origin='lower',extent=d['ext'],interpolation='gaussian',cmap=cmap,vmin=vr[0],vmax=vr[1])
    else:
        plt.imshow(d[fld],origin='lower',extent=d['ext'],interpolation='gaussian',cmap=cmap)
    plt.colorbar()
    if nCont != 0:
        if len(vr)==2:
            plt.contour(d['x'],d['y'],d[fld],nCont,colors='black',linewidths=0.5,vmin=vr[0],vmax=vr[1])
        else:
            plt.contour(d['x'],d['y'],d[fld],nCont,colors='black',linewidths=0.5)
    if 'time' in d:
        tstr = ('Time: %1.3e' % d['time'])
        plt.title(tstr,loc='left')
    plt.tight_layout()
    if fname != '':
        plt.savefig(fname)
        plt.close()
    else:
        plt.show()

# Save many plots for a given field split into frames through time
def saveFrames(gStr,fld):
    fldMin = sys.float_info.max
    fldMax = -sys.float_info.max
    for fStr in glob.iglob(gStr):
        d = dataFromFile(fStr)
        fldMin = min(np.min(d[fld]),fldMin)
        fldMax = max(np.max(d[fld]),fldMax)
    for fStr in glob.iglob(gStr):
        d = dataFromFile(fStr)
        ln = d['filename'].split('.')
        del ln[-1]
        fname = '.'.join(ln)+'_'+fld+'.png'
        plotField(d,fld,fname=fname,vr=[fldMin,fldMax])

def numericError(dc,df,fld):
    fx = df[fld].shape[1]
    fy = df[fld].shape[0]
    cx = dc[fld].shape[1]
    cy = dc[fld].shape[0]
    dx = (dc['ext'][1]-dc['ext'][0])/cx
    dy = (dc['ext'][3]-dc['ext'][2])/cy
    rx = int(fx/cx)
    ry = int(fy/cy)
    errfld = fld+'_err'
    dc[errfld] = np.zeros_like(dc[fld])
    # Verify layouts are compatible
    if rx!=ry or fx%rx+fy%ry!=0:
        print('Invalid refinement ratio\n')
        dc[errfld] = np.Nan*err
    # Compute error by averaging fine solution
    for j in range(0,cx):
        for i in range(0,cy):
            dc[errfld][i,j] = dc[fld][i,j]-np.average(df[fld][rx*i:rx*i+rx,rx*j:rx*j+rx])
    # Summarize
    return (dx*dy*np.sum(np.abs(dc[errfld])),np.max(np.abs(dc[errfld])))
    
# Calling convention: python3 gpplot.py <path/to/data.hdf5> <field name>
if __name__ == "__main__":
    # Open dataset
    print(sys.argv)
    d = dataFromFile(sys.argv[1])
    if len(sys.argv)>3:
        plotField(d,sys.argv[2],nCont=int(sys.argv[3]))
    else:
        plotField(d,sys.argv[2])

Download this code

Download the hdf5 data file

• A contour plot of the density can be generated by calling:

  python gpplot.py RayleighTaylor0128_3_002975.h5 dens
  

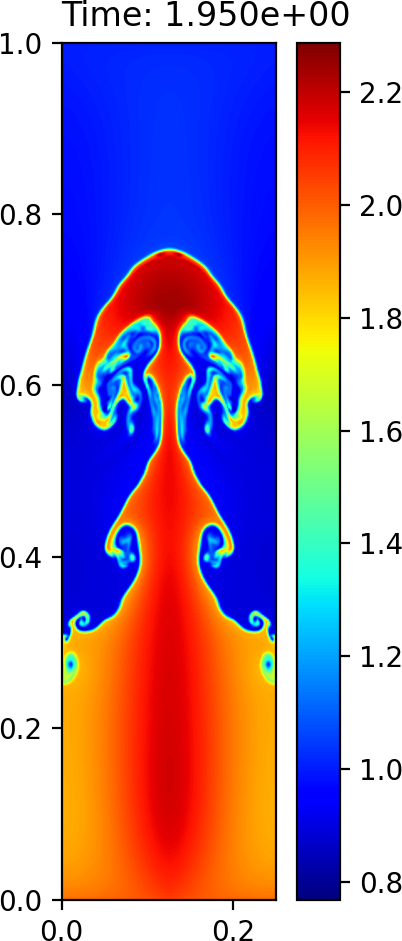
Plot of the density field at time \(T=1.95\) using imshow

• Line plots of the density along a couple slices can be generated as:

  import gpplot as gplt
  import numpy as np
  import matplotlib.pyplot as plt
  
  # Set fontsizes
  plt.rcParams.update({'axes.titlesize':16,'axes.labelsize':14,'xtick.labelsize':12,'ytick.labelsize':12})
  
  # Import data and extract fields into dictionary
  data = gplt.dataFromFile('RayleighTaylor0128_3_002975.h5')
  
  plt.figure()
  
  # 2 side-by-side subplots
  plt.subplot(1,2,1)
  plt.plot(data['dens'][:,64],data['y'],'-b',linewidth=2)
  plt.xlabel(r'$\rho$')
  plt.ylabel(r'$y$')
  plt.title(r'Density at $y=1/8$')
  plt.grid('both')
  
  plt.subplot(1,2,2)
  plt.plot(data['x'],data['dens'][300,:],'-b',linewidth=2)
  plt.xlabel(r'$x$')
  plt.ylabel(r'$\rho$')
  plt.title(r'Density at $x=0.586$')
  plt.grid('both')
  
  # Show plot on screen
  plt.show()
  

  Download this code

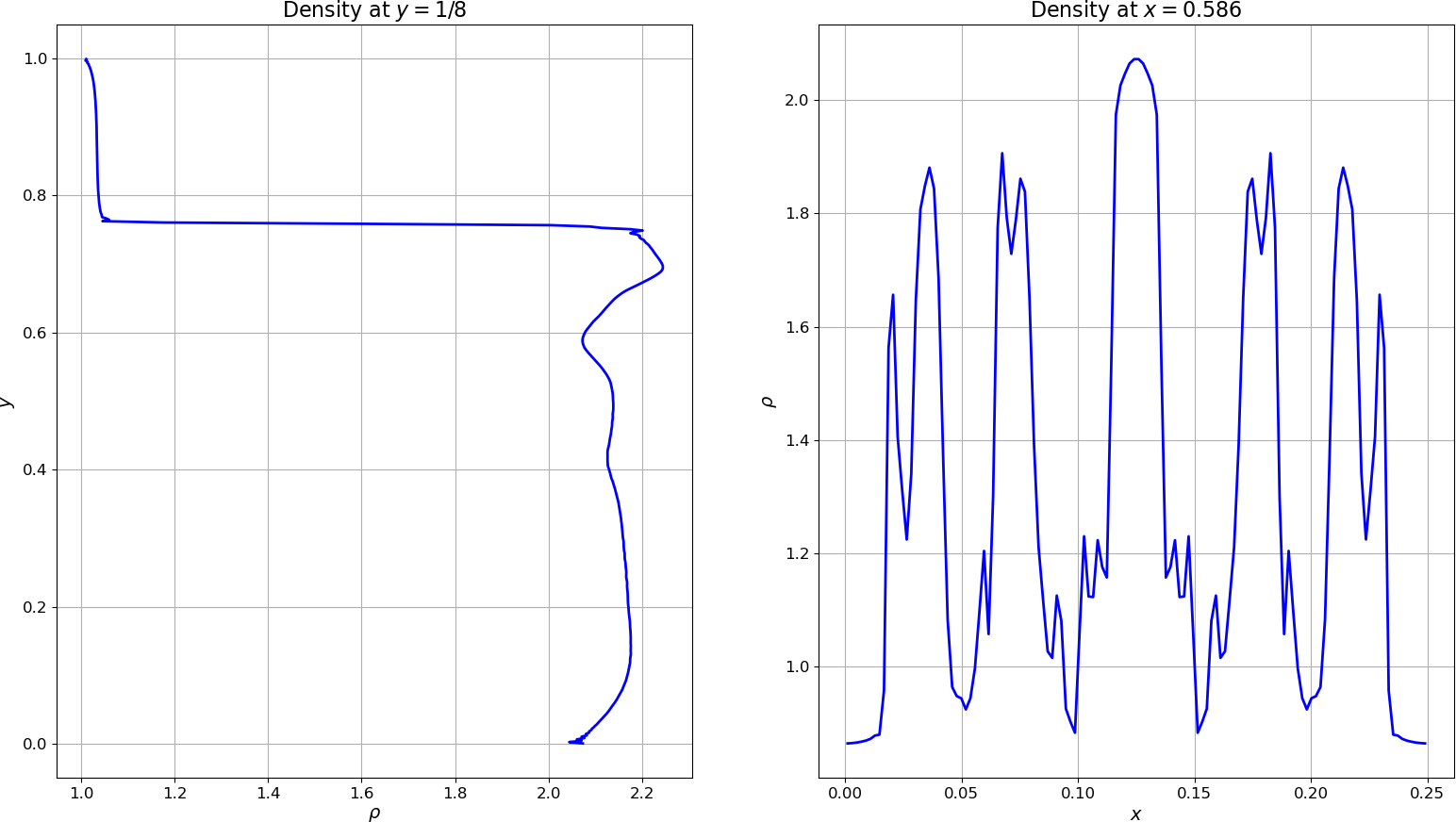
Density along slices of the flow

• A surface plot of the internal energy using plot_surface:

  import gpplot as gplt
  import numpy as np
  import matplotlib.pyplot as plt
  from matplotlib import cm
  
  # Set fontsizes
  plt.rcParams.update({'axes.titlesize':16,'axes.labelsize':14,'xtick.labelsize':12,'ytick.labelsize':12})
  
  # Import data and extract fields into dictionary
  data = gplt.dataFromFile('RayleighTaylor0128_3_002975.h5')
  
  # Create meshgrid from individual axes
  X,Y = np.meshgrid(data['x'],data['y'])
  
  # Create figure and 3D axes
  fig, ax = plt.subplots(subplot_kw={"projection": "3d"})
  ax.set_box_aspect((0.25,1,0.1))
  surf = ax.plot_surface(X, Y, data['eint'], cmap=cm.CMRmap, linewidth=0, antialiased=False)
  fig.colorbar(surf,shrink=0.4)
  
  # Show plot on screen
  plt.show()
  

  Download this code

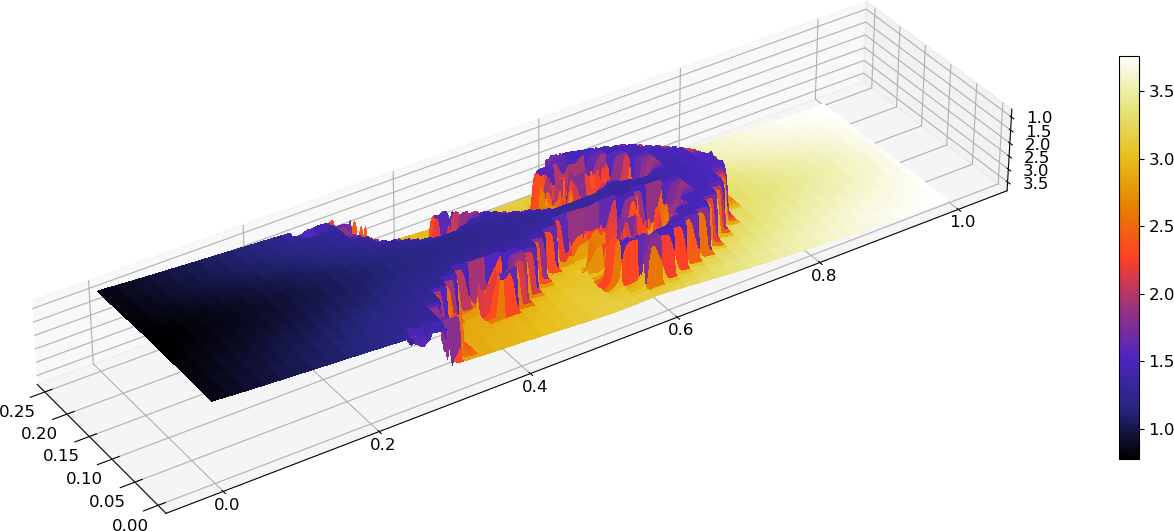
Surface plot of internal energy

• A wireframe plot of the pressure using plot_wireframe:

  import gpplot as gplt
  import numpy as np
  import matplotlib.pyplot as plt
  
  # Set fontsizes
  plt.rcParams.update({'axes.titlesize':16,'axes.labelsize':14,'xtick.labelsize':12,'ytick.labelsize':12})
  
  # Import data and extract fields into dictionary
  data = gplt.dataFromFile('RayleighTaylor0128_3_002975.h5')
  
  # Create meshgrid from individual axes
  X,Y = np.meshgrid(data['x'],data['y'])
  
  # Create figure and 3D axes
  fig, ax = plt.subplots(subplot_kw={"projection": "3d"})
  ax.set_box_aspect((0.25,1,0.3))
  ax.plot_wireframe(X, Y, data['pres'], rstride=4, cstride=4)
  
  # Show plot on screen
  plt.show()
  

  Download this code

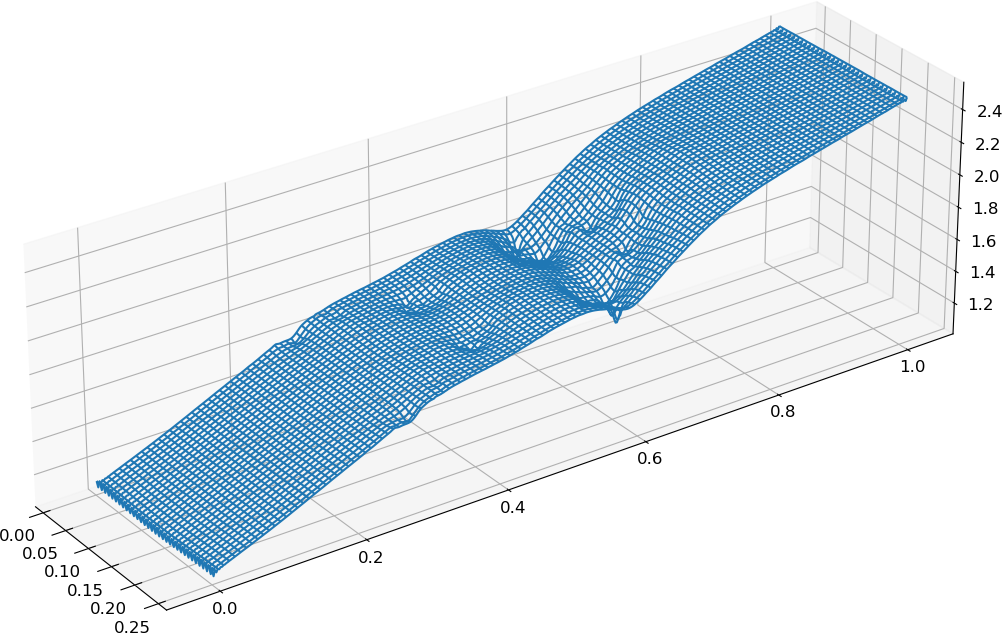
Wireframe plot of the pressure

One can also produce a plot with multiple subplots:

"""

/lectureNote/chapters/chapt05/codes/plot_flash_subplot.py

An example Python subplotting code using a FLASH 2d data
-- Sedov explosion on a uniform grid of size 256 x 256


See more examples and options at:

  http://matplotlib.org/gallery.html
  http://matplotlib.org/users/image_tutorial.html

Written by Prof. Dongwook Lee, for AMS 209, Fall.

"""


import h5py
import numpy as np
import os
import sys
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D


# =======================================
# 2D subplots

maxDens = -1.0
minDens = 1.e10
for i in range(1,7,1):
    fileName = 'sedov_hdf5_chk_000'+str(i)
    file = h5py.File(fileName, 'r')
    var  = file['dens']

    if var[0,0,:,:].max() > maxDens:
        maxDens = var[0,0,:,:].max()
        
    if var[0,0,:,:].min() < minDens:
        minDens = var[0,0,:,:].min()


fig,axes = plt.subplots(nrows=3,ncols=2)
print (fig,axes)

for i in range(1,7,1):
    print (i)
    fileName = 'sedov_hdf5_chk_000'+str(i)
    print (fileName)
    file = h5py.File(fileName, 'r')
    var  = file['dens']
    #plot_flash_2d_imshow(file)
    plt.subplot(3,2,i)
    plt.imshow(var[0,0,:,:],extent=[0,1,0,1],vmin=minDens,vmax=maxDens)
    plt.xlabel('$x$')
    plt.ylabel('$y$')
    #plt.title('2d plot of density')
    plt.colorbar()


    

# =======================================
# Show plots to screen
plt.show()

# close file
file.close()

Download this code

Download the data

Note

Notice in the above example that there are two for-loops, where the first loop finds the global min and max of the time varying densities over a series of times, \(t=0.01, 0.02, 0.03, 0.04, 0.05, 0.06\). The second loop uses the obtained minimum (\(\rho_{\min}\)) and maximum (\(\rho_{\max}\)) densities in order to plot six subfigures in a consistent color scheme. Otherwise, all six subfigures would use different color scales, making it hard to compare the density values over time.

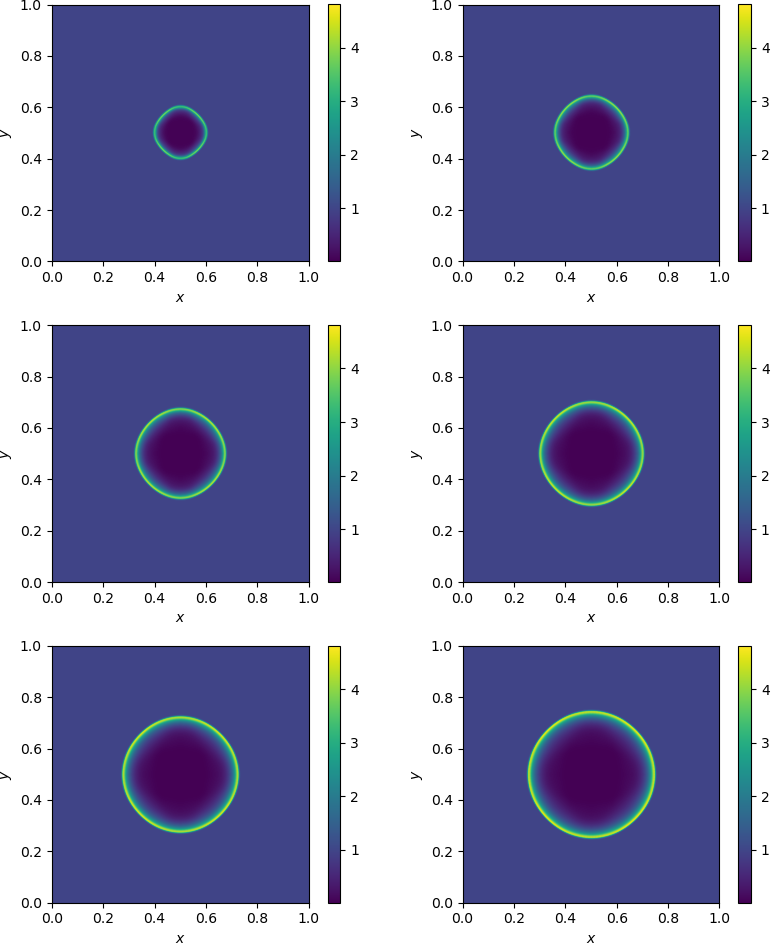
2D subplots of density at various times.

There is plenty more to learn, and many great examples can be found on the Matplotlib gallery page. If you have a mental image of a figure you want to create, have a look there first for anything that may be similar.

• Matplotlib homepage

• gallery

• pyplot commands