A short example of object-oriented programming (OOP) in Python¶
Python supports object-oriented programming (OOP). Some goals of OOP, among many others, are:
To package data and code together (encapsulation)
Organization of the code such that relevant parts are bundled together
Facilitate and ease interaction with more complex derived data types
An example: Polynomial interpolation¶
As a small example we’ll start by wrapping a univariate polynomial interpolation routine into a class. Initially this class will work for arbitrary points sets, though we’ll specialize it later. A straightforward implementation is:
1# File: polyInterp.py 2# Author: Ian May 3# Purpose: Implement a polynomial interpolation class as a way to demonstrate OOP 4# Notes: This is very much *not* the most efficient way to implement this 5 6import sys 7import numpy as np 8import matplotlib.pyplot as plt 9 10# Base polynomial interpolation class 11# Constructor takes in arbitrary distribution of nodes 12class PolyInterp: 13 def __init__(self, nodes): 14 # Copy in node positions 15 self.nodes = np.array(nodes) 16 # Set degree, number of nodes, and make space for coeffs 17 self.N = nodes.size 18 self.deg = self.N - 1 19 self.coeff = np.zeros(nodes.size) 20 # Build vandermonde matrix 21 self.V = np.zeros((self.N,self.N)) 22 for j in range(0,self.N): 23 self.V[:,j] = self.nodes**j 24 25 # Generate interpolant given data set 26 def interp(self, data): 27 self.coeff = np.linalg.solve(self.V,data) 28 29 # Evaluate interpolant at a set of point(s) 30 def evalInt(self, points): 31 interp = np.zeros(points.shape) 32 for j in range(0,self.N): 33 interp = interp + self.coeff[j]*points**j 34 return interp 35 36# Runge's function to test our interpolants on 37def runge(x): 38 return 1.0/(1.0 + 25.0*x**2) 39 40# Derivative of Runge's function to test our interpolants on 41def runge_der(x): 42 return -50.0*x/((1.0 + 25.0*x**2)**2) 43 44if __name__ == "__main__": 45 # Number of nodes to use (deg+1) 46 N = 9 47 if len(sys.argv)>1: 48 N = int(sys.argv[1]) 49 50 # Points to plot on 51 points = np.linspace(-1,1,300) 52 exact = runge(points) 53 54 # Construct interpolant using equispaced nodes 55 equi = PolyInterp(np.linspace(-1,1,N)) 56 equi.interp(runge(equi.nodes)) 57 eq_interp = equi.evalInt(points) 58 59 # Report maximum error 60 print('Max error for equispaced: ',np.max(np.abs(exact-eq_interp))) 61 62 # Create plot, cap y-limit for visibility 63 plt.plot(points,exact,'-k',points,eq_interp,'-r') 64 plt.plot(equi.nodes,runge(equi.nodes),'ro') 65 plt.legend(('Exact','Equispaced'),loc='best') 66 plt.title("Equispaced interpolation of Runge's function") 67 plt.grid('both') 68 plt.ylim([-0.1,1.1]) 69 plt.show() 70
In this example we can see a few salient features of OOP within Python. The class
PolyInterp has several functions (methods) defined within it. The first, and
most important, is the __init__ function, which accomplishes the following:
__init__defines all member data of the class. In this case the variables are as follows:nodes: Point locations where interpolants will be anchored toN: The number of interpolation locationsdeg: The degree of the underlying polynomial (this is alwaysN-1)V: The Vandermonde matrix associated to the given node set
__init__performs any set up required to instantiate a new object of the class. That is,__init__is the constructor
For __init__, and all other methods defined in the class, the first argument
is always self. This gives a way for the method to act on member variables of
the class that belong to distinct objects. That is, different objects instantiated
from the same class will have different internal data (this is encapsulation).
Note however, that when instantiating an object the self argument is implied,
and need not be written (nor could it be). Similarly when calling methods on existing
objects the self argument is implied. Alternatively, you can call a class method
and pass an object as self. Consider the following snippet:
>>> import numpy as np
>>> from PolyInterp import PolyInterp
>>> equi = PolyInterp(np.linspace(-1,1,9))
>>> data = np.random.rand(9)
>>> # The following two are completely equivalent
>>> equi.interp(data)
>>> PolyInterp.interp(equi,data)
As a touchstone to something we did before, consider having a NumPy array called arr.
We could get the maximum value of this array by calling either arr.max() or
np.max(arr).
Running this code using the default setting of 9 equispaced nodes in the interval \([-1,1]\) should produce the following output and figure.
$ python PolyInterp.py
Max error for equispaced: 1.0451573170836823
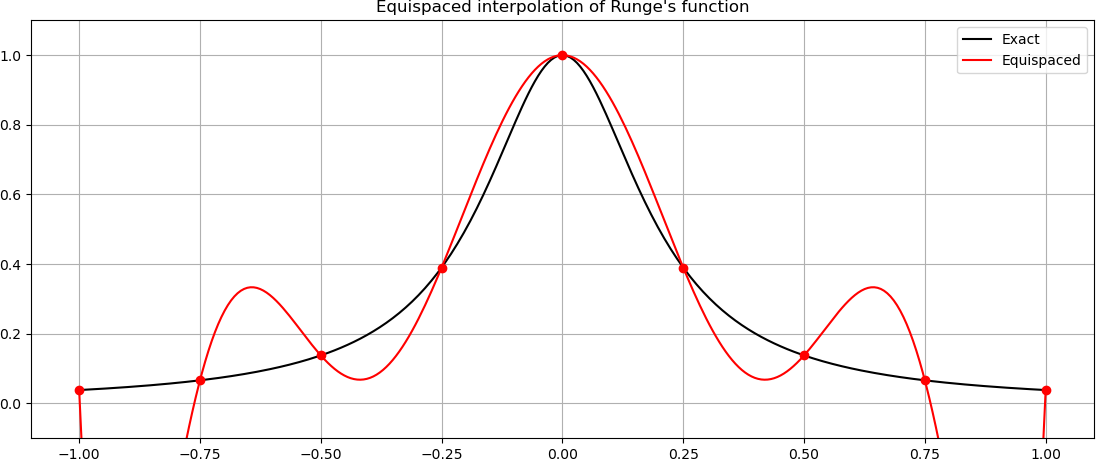
Interpolation of Runge’s function using an equispaced grid of points. Note that the vertical axis is truncated to avoid the oscillations near boundaries dominating the figure.¶
Inheritance and Chebyshev interpolation¶
Specifying the nodes for interpolation everytime is a bit tedious. Perhaps more importantly, there are node sets with very different behaviors regarding interpolation quality. The equispaced nodes we used in the previous example are incredibly bad. A much better set is given by the Chebyshev nodes:
Rather than generating these nodes everytime we need them, we can create a class specifically for Chebyshev interpolation. However, we’ve already written a bit of code for interpolation, and it seems wasteful to re-write all the parts that are the same.
A nice solution is to use inheritance. We’ll create ChebyInterp as a specialization
of the PolyInterp class. In this way ChebyInterp will inherit all of the member
functions and data members from the parent class PolyInterp, and we can override items as
needed. The code to accomplish this is as follows:
1# File: ChebyInterp.py 2# Author: Ian May 3# Purpose: Specialize the PolyInterp class to Chebyshev interpolation 4# to demonstrate inheritance 5# Notes: This is very much *not* the most efficient way to implement this 6 7import sys 8import numpy as np 9import matplotlib.pyplot as plt 10 11from PolyInterp import PolyInterp, runge, runge_der 12 13# Chebyshev polynomial interpolation, specializes PolyInterp 14# Constructor requires number of points desired 15class ChebyInterp(PolyInterp): 16 def __init__(self, N): 17 # Invoke PolyInterp constructor using Chebyshev nodes 18 k = np.arange(1,2*N,2) # Odd nums up to 2*N 19 PolyInterp.__init__(self, np.cos(np.pi*k/(2.0*N))) 20 21if __name__ == "__main__": 22 # Number of nodes to use (deg+1) 23 N = 9 24 if len(sys.argv)>1: 25 N = int(sys.argv[1]) 26 27 # Points to plot on 28 points = np.linspace(-1,1,300) 29 exact = runge(points) 30 31 # Construct interpolant using equispaced nodes 32 equi = PolyInterp(np.linspace(-1,1,N)) 33 equi.interp(runge(equi.nodes)) 34 eq_interp = equi.evalInt(points) 35 36 # Construct interpolant using Chebyshev nodes 37 cheb = ChebyInterp(N) 38 cheb.interp(runge(cheb.nodes)) 39 cv_interp = cheb.evalInt(points) # function inherited from base class 40 41 # Report maximum error 42 print('Max error for equispaced: ',np.max(np.abs(exact-eq_interp))) 43 print('Max error for Chebyshev: ',np.max(np.abs(exact-cv_interp))) 44 45 # Create plot, cap y-limit for visibility 46 plt.plot(points,exact,'-k',points,eq_interp,'-r',points,cv_interp,'-b') 47 plt.plot(equi.nodes,runge(equi.nodes),'ro',cheb.nodes,runge(cheb.nodes),'bs') 48 plt.legend(('Exact','Equispaced','Chebyshev'),loc='best') 49 plt.title('Comparison of equispaced and Chebyshev interpolation') 50 plt.grid('both') 51 plt.ylim([-0.1,1.1]) 52 plt.show() 53
The primary lines of interest are 15 and 19. When declaring the ChebyInterp class on line
15 we pass the PolyInterp class to indicate that it is contained within this new one.
Then, inside the __init__ function we construct the Chebyshev nodes, and forward them to
the __init__ function for the underlying PolyInterp class (line 19).
Most of this is just a main function to play around with the classes we’ve created. The
definition of the ChebyInterp class actually required only four lines!
Running this code using the default setting of 9 nodes should produce the following output and figure.
$ python PolyInterp.py
Max error for equispaced: 1.0451573170836823
Max error for Chebyshev: 0.17073385326790647
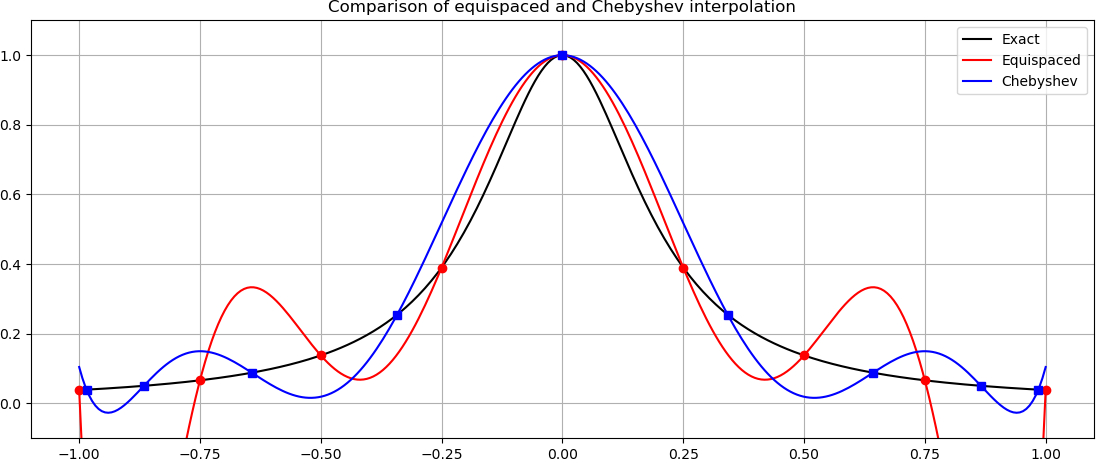
Interpolation of Runge’s function using both equispaced nodes and Chebyshev nodes. Note that the Chebyshev interpolant strongly resists oscillation near the boundaries compared to the interpolant over equispaced points¶
There is plenty more to learn about objected oriented programming in Python. These examples are meant to be rather small and easily approachable. A good starting point for deeper study is the tutorial on the Python website:
Exercises¶
Try running the
ChebyInterpexample for different numbers of nodes. Note that the main function will pull in a command line argument to make this easier. What can you observe?Try growing the interval where the interpolants are evaluated. Does the superior performance of Chebyshev interpolation continue now that we are extrapolating the function?
Add a method to the
PolyInterpclass to evaluate the derivative of the interpolant. Observe that we can use it onChebyInterpobjects without changing theChebyInterpclass definition at all.
